Clustering and routing: Difference between revisions
(Added Kaur and System Diagram) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 43: | Line 43: | ||
|} | |} | ||
Since routing protocols with intelligence improves network lifetime more than traditional approaches for WSN applications, we decided to implement RL-based protocols, and consider CLIQUE protocol<ref>A. Förster and A. L. Murphy, “CLIQUE: Role-free clustering with Q-learning for wireless sensor networks,” in Proceedings of International Conference on Distributed Computing Systems, 2009, pp. 441–449.</ref> and the Deep Q-Network protocol by Kaur et al<ref>G. Kaur, P. Chanak, and M. Bhattacharya, “Energy-Efficient Intelligent Routing Scheme for IoT-Enabled WSNs,” IEEE Internet of Things Journal, vol. 8, no. 14, pp. 11440–11449, Jul 2021.</ref>. For our baseline protocol, we choose the LEACH protocol<ref>W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “An application-specific protocol architecture for wireless microsensor networks,” IEEE Transactions on Wireless Communications, vol. 1, no. 4, pp. 660–670, Oct 2002.</ref> as it is one of the pioneering clustering and routing approaches for WSNs. | Since routing protocols with intelligence improves network lifetime more than traditional approaches for WSN applications, we decided to implement RL-based protocols, and consider CLIQUE protocol<ref>A. Förster and A. L. Murphy, “CLIQUE: Role-free clustering with Q-learning for wireless sensor networks,” in Proceedings of International Conference on Distributed Computing Systems, 2009, pp. 441–449.</ref> and the Deep Q-Network protocol by Kaur et al<ref>G. Kaur, P. Chanak, and M. Bhattacharya, “Energy-Efficient Intelligent Routing Scheme for IoT-Enabled WSNs,” IEEE Internet of Things Journal, vol. 8, no. 14, pp. 11440–11449, Jul 2021.</ref>. For our baseline protocol, we choose the LEACH protocol<ref>W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “An application-specific protocol architecture for wireless microsensor networks,” IEEE Transactions on Wireless Communications, vol. 1, no. 4, pp. 660–670, Oct 2002.</ref> as it is one of the pioneering clustering and routing approaches for WSNs. | ||
== LEACH Protocol == | |||
One of the pioneering clustering and routing approaches for WSNs is the Low Energy Adaptive Clustering Hierarchy (LEACH). One of the pioneering clustering and routing approaches for WSNs is LEACH. In LEACH, the idea is to select the cluster heads by rotation so that the high energy dissipation in communicating with the base station is spread across all sensor nodes in the network. | |||
The operation of the LEACH protocol is broken into multiple rounds, where each round has two phases: set-up phase and steady-state phase. In the set-up phase, cluster heads are selected and clusters are formed. In the steady-state phase, member nodes send their data to the respective cluster heads, and the cluster heads perform data aggregation for transmission to the base station. The duration of the steady-state phase is typically longer than that of the set-up phase in order to minimize the overhead due to cluster formation. | |||
During the set-up phase, each node decides whether or not to become a cluster head (CH) for the current round. This decision is made by the node choosing a random number between 0 and 1. If the number is less than the following threshold, T(n), the node becomes a cluster head: | |||
<math>T(n) = f(n) = \begin{cases} \frac{P}{1-P(r\bmod \frac{1}{P})}, & \text{if }n \in G \\ 0, & \text{otherwise} \end{cases}</math> | |||
where P is the desired percentage of cluster heads, r is the current round, and G is the set of nodes that have not been elected as cluster heads in the last 1/P rounds. Based on the algorithm, this protocol ensures load balancing by preventing a node from being selected as a cluster head for multiple consecutive rounds. | |||
After the cluster heads are determined, each elected cluster head then broadcasts an advertisement message so that the remaining nodes in the network can choose which cluster to join based on the received signal strength of each message. Each node sends a join request message to its chosen cluster head. After which, the cluster head creates a TDMA schedule, and assigns each node in its cluster a time slot to transmit the data. | |||
Once the clusters are formed, the network can now proceed to the steady-state phase for data transmission. After some time spent on the steady-state phase, the network goes back into the set-up phase for another round of cluster formation. | |||
== CLIQUE == | |||
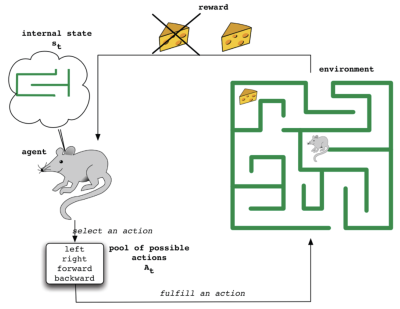
[[File:Reinforcement_Learning_Model.png|thumb|400x400px|Figure 2. Reinforcement Learning Model Which Involves an Agent Taking Actions in an Environment.]] | |||
CLIQUE is a cluster-based reinforcement learning (RL) algorithm based on Q-learning. Although it is a cluster-based algorithm, CLIQUE is different from traditional clustering approaches, such as LEACH. It removes the cluster head (CH) election process altogether, and thus its overhead in terms of communication and energy consumption. CLIQUE does this by employing reinforcement learning and enabling a node to independently decide whether or not to act as a CH. | |||
A reinforcement learning model, as shown in Figure 2, involves an agent taking actions in an environment so as to maximize the notion of cumulative reward.<ref>R. V. Kulkarni, A. Forster, and G. K. Venayagamoorthy, “Computational intelligence in wireless sensor networks: A survey,” IEEE Communications Surveys and Tutorials, vol. 13, no. 1, pp. 68–96, 2011.</ref> In the context of routing problems in WSNs, the agents are the nodes themselves. When it is scheduled to transmit a packet, a node (selects an action or) chooses one of its neighbors as the next hop, so that the total routing cost (or reward) from the source node to the destination node is minimized. To determine these routing costs, CLIQUE employs the Q-learning algorithm. | |||
Q-learning is a model-free RL algorithm that allows an agent to learn the goodness (or value) of an action in a particular state without requiring a model of the environment (hence, model-free). It does this by using the Bellman optimality equation to compute a value for each state-action pair, | |||
<math>Q(S,A) \leftarrow Q(S,A) + \alpha\Bigl(R + \gamma \underset{a'}{max} Q(S',a') - Q(S,A)\Bigr)</math> | |||
where Q(S,A) is the Q-value for a given state-action pair, R is the immediate reward, <math>\alpha</math> is the learning rate, and <math>\gamma</math> is the discount factor. By applying this equation iteratively, the real Q-values are learned over time. In most RL problems, the action with the highest Q-value for a given state is the best action. In routing, these Q-values are the routing costs, and the neighbor with the best Q-value (or minimum routing cost) is the next hop for an optimal route. These Q-values or routing costs in CLIQUE are calculated based on the following parameters: hop count and battery level of the nodes. The hop count aims to minimize the communication overhead for better energy efficiency, while the battery status ensures that low-powered nodes are avoided in the transmission path. | |||
It is assumed that there are multiple sinks in the network, and that DATA packets generated by nodes should be transmitted to all sinks. It is also assumed that each node in the network knows which cluster it belongs to. Instead of identifying the CHs with an election process, each node makes a simple decision whether or not to act as a CH based on the Q-values. The node with the best Q-value (or lowest routing cost to all sinks) in a cluster is considered the cluster head. As such, it must aggregate all data from the other nodes in its cluster, and route this aggregated data to the sinks. Nodes that are not identified as cluster heads must route this data to another suited neighbor, towards the identified cluster head. By using Q-learning, the Q-values, and hence the cluster heads, are incrementally learned. And so, in CLIQUE, we are solving the intra-cluster routing problem, from a source node to a cluster head. The inter-cluster routing problem, from the cluster head to the sinks, can be solved by using any multi-hop routing approach. | |||
Before learning begins, the Q-values are initialized first. These values may actually be any random values, and Q-learning should be able to converge to the optimal Q-values (or real routing costs). However, to speed up the learning process, we can initialize the Q-values close to the optimal Q-values. In CLIQUE, the Q-value of an action are initialized based on the approximate routing costs as follows: | |||
<math>Q(A_{n_i}) = Q_{hops}(A_{n_i}) * Q_{battery}(A_{n_i}) | |||
= \sum_{d \in D} \text{hops}_d^{n_i} * \text{hcm} (\text{bat}_{n_i})</math> | |||
where D is the set of sinks, <math>\text{hops}_d^{n_i}</math> is the number of hops neighbor <math>n_i</math> needs to reach sink d, and hcm is the hop count multiplier. We can see here that the lower the hop count is, the lower the Q-value or routing cost is. In estimating the hop count, it is assumed in CLIQUE that sinks flood the network with DATA_REQUEST packets to indicate their data interest. As this packet propagates in the network, each node knows some routing information to all sinks, including the hop count and battery status. On the other hand, the hcm( ) is a function whose value exponentially increases with decreasing battery levels. Hence, nodes with lower battery levels have higher hcm( ) values, and thus higher Q-values or higher routing costs. | |||
Once the Q-values are initialized, the learning process begins. Here, we use the Bellman optimality equation iteratively to learn the real Q-values. In CLIQUE, since the Q-values are initialized to the approximate routing costs, the learning rate () is set to 1 for faster learning process. The immediate reward (R) is the cost of reaching a neighbor, and is always 1 in the RL model. The discount factor () is also set to 1 to account for future rewards. And since Q-values are routing costs, minimum Q-values are desired. With this, the equation for updating a Q-value is given by: | |||
<math>Q(S,A) \leftarrow 1 + \underset{a'}{min} Q(S',a')</math> | |||
In order to learn these Q-values, neighboring nodes exchange information. To reduce communication costs, these Q-values are piggybacked on normal DATA packets as feedback information, which allows for any downstream node (node that received the DATA packet) to update routing costs or Q-values at its upstream node (node from previous hop that sent the DATA packet) using the Bellman optimality equation. By sending and receiving this feedback information among neighboring nodes, the information is propagated through the network, and the real routing costs are learned over time without the need for a global knowledge of the network. | |||
== Deep Q-Network protocol by Kaur et al. == | |||
As the number of neighbors (or state-action pairs) increases, the number of Q-values that are needed to be stored in the memory also increases, hence requiring a larger memory. For these routing problems, look-up table (LUT)-based algorithms, such as Q-learning, may no longer be practical. Instead, we train a function approximator, like a neural network, to achieve the same result of mapping each state-action pair to a Q-value. And, since we are now integrating deep learning to solve RL problems, these are typically called deep reinforcement learning algorithms. | |||
Deep Q-network (DQN) is a deep RL algorithm based on Q-learning. Here, we estimate the Q-values by minimizing the loss at each step i given by the following equation using gradient descent: | |||
<math>L_i(w_i) = \Epsilon_{s,a,r,s' \sim D_i} \left [ \Bigl(r + \gamma \underset{a'}{max} Q(s',a';w_i^\text{-}) - Q(s,a;w_i)\Bigr) ^2 \right ]</math> | |||
where <math>L_i(w_i)</math> is the loss function, <math>Q(s,a;w_i)</math> is the approximate Q-value, and <math>r + \gamma max Q</math> is the Q-learning target, which is similar to the standard Q-learning target. However, updating the network (or the parameters of the network) incrementally at each time step using the latest transition (or data) may result in instability, where parameters can diverge.<ref>V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. A. Riedmiller, “Playing Atari with Deep Reinforcement Learning,” ArXiv, vol. abs/1312.5602, 2013.</ref> Instead, we compute the loss and its gradient using a mini-batch of transitions that are randomly sampled from what is called a replay memory, which essentially stores the transitions or data we have seen thus far. This technique, called experience replay, improves data efficiency by allowing a transition to be reused in multiple network updates, and ensures stability by removing correlation on the transition sequence (randomly sampled transitions are less likely to be correlated). | |||
Aside from experience replay, a deep Q-network also uses fixed Q-targets for a more stable network update. It does this by maintaining two different networks, as is shown in the given loss function above (where there are two sets of parameters or weights). One network, also known as the Q-network, is used to predict the approximate Q-value, and is trained based on the loss function. The other network, which is called the target network, is fixed and not updated, and is used to estimate the Q-learning target. In the loss equation, <math>w_i^-</math> denotes that the parameters are not updated. By keeping this network frozen, we ensure that the target Q-values are stable (and thus, stable Q-network update). However, since the target Q-values are predictions after all, the target network is periodically synchronized with the main Q-network. | |||
Kaur’s work utilizes DQN to solve the routing problem in WSNs. Unlike CLIQUE, it solves both the intra-cluster and inter-cluster routing problems. For the intra-cluster routing, the Q-values are optimized based on the following conflicting objectives: maximize the lifetime of the nodes, maximize network throughput, and minimize the communication delay. The inter-clustering routing is also solved using multi-objective deep RL, where we minimize the load on the CH, maximize the network throughput, and minimize the communication delay. | |||
[[File:System Diagram of Clustering and Routing Block.png|thumb|500x500px|Figure 3. System Diagram for Clustering and Routing Block.]] | |||
In this work, the network is heterogeneous, where the CHs, also called as supernodes, have higher energy than the other nodes. This work also proposes an unequal clustering scheme. The CHs near the sink (or base station) will typically consume more energy since they have to collect data from their cluster members, and from the other cluster heads for inter-cluster routing. To solve this problem, clusters near the sink are assigned a lower cluster radius (and thus smaller number of cluster members) than those far from the sink. By combining this clustering scheme and deep Q-network, Kaur’s work is able to outperform other RL-based routing algorithms. | |||
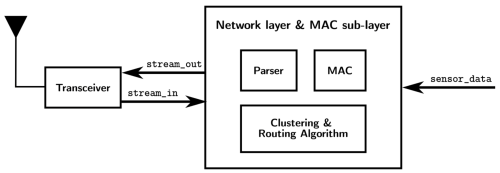
== System Diagram == | |||
Figure 3 shows how each node is modeled, from input stream to output stream. The Carrier-sense Multiple Access with Collision Avoidance (CSMA-CA) protocol, which is used to avoid collision of packets, is handled by the MAC block. The data stream, which uses the IEEE 802.15.4 packet format, will be processed by the parser block and the corresponding information is sent to the clustering and routing protocol block. | |||
=== References === | === References === | ||
Latest revision as of 14:27, 28 June 2023
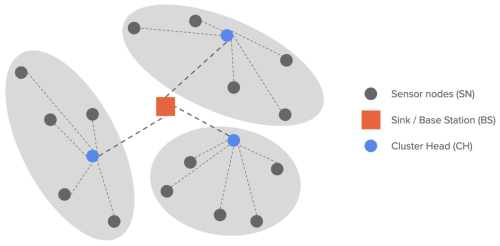
Routing protocols in wireless sensor networks (WSNs) are generally classified into three main categories according to network structure: flat, hierarchical, and location-based.[1][2] In flat routing protocols, all nodes in the network are typically assigned equal roles, where each node senses the environment and sends the sensed data to a sink or base station. In hierarchical routing protocols, nodes are grouped into clusters. Each cluster has its own cluster head and member nodes, as shown in Figure 1. The member nodes still play the same role of sensing the environment. They forward their sensed data to the respective cluster heads (instead of the base station) for aggregation, and the cluster heads are the ones responsible for transmitting the aggregated data to the base station. In comparison to flat routing protocols, hierarchical routing protocols offer several advantages, including higher energy efficiency, increased scalability, and increased robustness, all of which are advantageous for WSNs.[3]
Computational Intelligence Paradigms
Different computational intelligence (CI) paradigms that can be applied in solving clustering and routing in WSNs are shown in Table 1. Among these paradigms, reinforcement learning (RL) is the most appropriate for WSN applications as it has been proven to achieve optimal routing results in WSNs.[4] While it may need some time to learn the optimal routes, it is highly flexible to network topology changes. Moreover, it has low processing requirements, and low-cost or simple implementation. This makes RL suitable for energy-efficient routing at individual nodes, despite having medium memory requirements for keeping track of different possible actions and values. Thus, discussions on routing protocols with computational intelligence were focused on RL-based routing protocols.
| CI Paradigms | Computational Requirements | Memory Requirements | Flexibility | Clustering & Routing |
|---|---|---|---|---|
| Neural Network | medium | medium | low | less appropriate |
| Fuzzy Logic | medium | medium | high | moderately appropriate |
| Evolutionary Algorithm | medium | high | low | less appropriate |
| Swarm Intelligence | low | medium | high | moderately appropriate |
| Reinforcement Learning | low | medium | high | most appropriate |
Since routing protocols with intelligence improves network lifetime more than traditional approaches for WSN applications, we decided to implement RL-based protocols, and consider CLIQUE protocol[6] and the Deep Q-Network protocol by Kaur et al[7]. For our baseline protocol, we choose the LEACH protocol[8] as it is one of the pioneering clustering and routing approaches for WSNs.
LEACH Protocol
One of the pioneering clustering and routing approaches for WSNs is the Low Energy Adaptive Clustering Hierarchy (LEACH). One of the pioneering clustering and routing approaches for WSNs is LEACH. In LEACH, the idea is to select the cluster heads by rotation so that the high energy dissipation in communicating with the base station is spread across all sensor nodes in the network.
The operation of the LEACH protocol is broken into multiple rounds, where each round has two phases: set-up phase and steady-state phase. In the set-up phase, cluster heads are selected and clusters are formed. In the steady-state phase, member nodes send their data to the respective cluster heads, and the cluster heads perform data aggregation for transmission to the base station. The duration of the steady-state phase is typically longer than that of the set-up phase in order to minimize the overhead due to cluster formation.
During the set-up phase, each node decides whether or not to become a cluster head (CH) for the current round. This decision is made by the node choosing a random number between 0 and 1. If the number is less than the following threshold, T(n), the node becomes a cluster head:
where P is the desired percentage of cluster heads, r is the current round, and G is the set of nodes that have not been elected as cluster heads in the last 1/P rounds. Based on the algorithm, this protocol ensures load balancing by preventing a node from being selected as a cluster head for multiple consecutive rounds.
After the cluster heads are determined, each elected cluster head then broadcasts an advertisement message so that the remaining nodes in the network can choose which cluster to join based on the received signal strength of each message. Each node sends a join request message to its chosen cluster head. After which, the cluster head creates a TDMA schedule, and assigns each node in its cluster a time slot to transmit the data.
Once the clusters are formed, the network can now proceed to the steady-state phase for data transmission. After some time spent on the steady-state phase, the network goes back into the set-up phase for another round of cluster formation.
CLIQUE
CLIQUE is a cluster-based reinforcement learning (RL) algorithm based on Q-learning. Although it is a cluster-based algorithm, CLIQUE is different from traditional clustering approaches, such as LEACH. It removes the cluster head (CH) election process altogether, and thus its overhead in terms of communication and energy consumption. CLIQUE does this by employing reinforcement learning and enabling a node to independently decide whether or not to act as a CH.
A reinforcement learning model, as shown in Figure 2, involves an agent taking actions in an environment so as to maximize the notion of cumulative reward.[9] In the context of routing problems in WSNs, the agents are the nodes themselves. When it is scheduled to transmit a packet, a node (selects an action or) chooses one of its neighbors as the next hop, so that the total routing cost (or reward) from the source node to the destination node is minimized. To determine these routing costs, CLIQUE employs the Q-learning algorithm.
Q-learning is a model-free RL algorithm that allows an agent to learn the goodness (or value) of an action in a particular state without requiring a model of the environment (hence, model-free). It does this by using the Bellman optimality equation to compute a value for each state-action pair,
where Q(S,A) is the Q-value for a given state-action pair, R is the immediate reward, is the learning rate, and is the discount factor. By applying this equation iteratively, the real Q-values are learned over time. In most RL problems, the action with the highest Q-value for a given state is the best action. In routing, these Q-values are the routing costs, and the neighbor with the best Q-value (or minimum routing cost) is the next hop for an optimal route. These Q-values or routing costs in CLIQUE are calculated based on the following parameters: hop count and battery level of the nodes. The hop count aims to minimize the communication overhead for better energy efficiency, while the battery status ensures that low-powered nodes are avoided in the transmission path.
It is assumed that there are multiple sinks in the network, and that DATA packets generated by nodes should be transmitted to all sinks. It is also assumed that each node in the network knows which cluster it belongs to. Instead of identifying the CHs with an election process, each node makes a simple decision whether or not to act as a CH based on the Q-values. The node with the best Q-value (or lowest routing cost to all sinks) in a cluster is considered the cluster head. As such, it must aggregate all data from the other nodes in its cluster, and route this aggregated data to the sinks. Nodes that are not identified as cluster heads must route this data to another suited neighbor, towards the identified cluster head. By using Q-learning, the Q-values, and hence the cluster heads, are incrementally learned. And so, in CLIQUE, we are solving the intra-cluster routing problem, from a source node to a cluster head. The inter-cluster routing problem, from the cluster head to the sinks, can be solved by using any multi-hop routing approach.
Before learning begins, the Q-values are initialized first. These values may actually be any random values, and Q-learning should be able to converge to the optimal Q-values (or real routing costs). However, to speed up the learning process, we can initialize the Q-values close to the optimal Q-values. In CLIQUE, the Q-value of an action are initialized based on the approximate routing costs as follows:
where D is the set of sinks, is the number of hops neighbor needs to reach sink d, and hcm is the hop count multiplier. We can see here that the lower the hop count is, the lower the Q-value or routing cost is. In estimating the hop count, it is assumed in CLIQUE that sinks flood the network with DATA_REQUEST packets to indicate their data interest. As this packet propagates in the network, each node knows some routing information to all sinks, including the hop count and battery status. On the other hand, the hcm( ) is a function whose value exponentially increases with decreasing battery levels. Hence, nodes with lower battery levels have higher hcm( ) values, and thus higher Q-values or higher routing costs.
Once the Q-values are initialized, the learning process begins. Here, we use the Bellman optimality equation iteratively to learn the real Q-values. In CLIQUE, since the Q-values are initialized to the approximate routing costs, the learning rate () is set to 1 for faster learning process. The immediate reward (R) is the cost of reaching a neighbor, and is always 1 in the RL model. The discount factor () is also set to 1 to account for future rewards. And since Q-values are routing costs, minimum Q-values are desired. With this, the equation for updating a Q-value is given by:
In order to learn these Q-values, neighboring nodes exchange information. To reduce communication costs, these Q-values are piggybacked on normal DATA packets as feedback information, which allows for any downstream node (node that received the DATA packet) to update routing costs or Q-values at its upstream node (node from previous hop that sent the DATA packet) using the Bellman optimality equation. By sending and receiving this feedback information among neighboring nodes, the information is propagated through the network, and the real routing costs are learned over time without the need for a global knowledge of the network.
Deep Q-Network protocol by Kaur et al.
As the number of neighbors (or state-action pairs) increases, the number of Q-values that are needed to be stored in the memory also increases, hence requiring a larger memory. For these routing problems, look-up table (LUT)-based algorithms, such as Q-learning, may no longer be practical. Instead, we train a function approximator, like a neural network, to achieve the same result of mapping each state-action pair to a Q-value. And, since we are now integrating deep learning to solve RL problems, these are typically called deep reinforcement learning algorithms.
Deep Q-network (DQN) is a deep RL algorithm based on Q-learning. Here, we estimate the Q-values by minimizing the loss at each step i given by the following equation using gradient descent:
where is the loss function, is the approximate Q-value, and is the Q-learning target, which is similar to the standard Q-learning target. However, updating the network (or the parameters of the network) incrementally at each time step using the latest transition (or data) may result in instability, where parameters can diverge.[10] Instead, we compute the loss and its gradient using a mini-batch of transitions that are randomly sampled from what is called a replay memory, which essentially stores the transitions or data we have seen thus far. This technique, called experience replay, improves data efficiency by allowing a transition to be reused in multiple network updates, and ensures stability by removing correlation on the transition sequence (randomly sampled transitions are less likely to be correlated).
Aside from experience replay, a deep Q-network also uses fixed Q-targets for a more stable network update. It does this by maintaining two different networks, as is shown in the given loss function above (where there are two sets of parameters or weights). One network, also known as the Q-network, is used to predict the approximate Q-value, and is trained based on the loss function. The other network, which is called the target network, is fixed and not updated, and is used to estimate the Q-learning target. In the loss equation, denotes that the parameters are not updated. By keeping this network frozen, we ensure that the target Q-values are stable (and thus, stable Q-network update). However, since the target Q-values are predictions after all, the target network is periodically synchronized with the main Q-network.
Kaur’s work utilizes DQN to solve the routing problem in WSNs. Unlike CLIQUE, it solves both the intra-cluster and inter-cluster routing problems. For the intra-cluster routing, the Q-values are optimized based on the following conflicting objectives: maximize the lifetime of the nodes, maximize network throughput, and minimize the communication delay. The inter-clustering routing is also solved using multi-objective deep RL, where we minimize the load on the CH, maximize the network throughput, and minimize the communication delay.
In this work, the network is heterogeneous, where the CHs, also called as supernodes, have higher energy than the other nodes. This work also proposes an unequal clustering scheme. The CHs near the sink (or base station) will typically consume more energy since they have to collect data from their cluster members, and from the other cluster heads for inter-cluster routing. To solve this problem, clusters near the sink are assigned a lower cluster radius (and thus smaller number of cluster members) than those far from the sink. By combining this clustering scheme and deep Q-network, Kaur’s work is able to outperform other RL-based routing algorithms.
System Diagram
Figure 3 shows how each node is modeled, from input stream to output stream. The Carrier-sense Multiple Access with Collision Avoidance (CSMA-CA) protocol, which is used to avoid collision of packets, is handled by the MAC block. The data stream, which uses the IEEE 802.15.4 packet format, will be processed by the parser block and the corresponding information is sent to the clustering and routing protocol block.
References
- ↑ N. Al-Karaki and A. E. Kamal, “Routing techniques in wireless sensor networks: A survey,” IEEE Wireless Communications, vol. 11, pp. 6–28, 12 2004.
- ↑ N. A. Pantazis, S. A. Nikolidakis, and D. D. Vergados, “Energy-efficient routing protocols in wireless sensor networks: A survey,” IEEE Communications Surveys & Tutorials, vol. 15, pp. 551–591, 2013.
- ↑ Raghavendra V. Kulkarni, Anna Forster, and Ganesh Kumar Venayagamoorthy. “Computational Intelligence in Wireless Sensor Networks: A Survey”. In: IEEE Communications Surveys & Tutorials 13.1 (2011), pp. 68–96. doi: 10.1109/SURV.2011.040310.00002.
- ↑ Mohammad Abu Alsheikh et al. “Machine Learning in Wireless Sensor Networks: Algorithms, Strategies, and Applications”. In: IEEE Communications Surveys & Tutorials 16.4 (2014), pp. 1996–2018. doi: 10.1109/COMST.2014.2320099.
- ↑ Raghavendra V. Kulkarni, Anna Forster, and Ganesh Kumar Venayagamoorthy. “Computational Intelligence in Wireless Sensor Networks: A Survey”. In: IEEE Communications Surveys & Tutorials 13.1 (2011), pp. 68–96. doi: 10.1109/SURV.2011.040310.00002.
- ↑ A. Förster and A. L. Murphy, “CLIQUE: Role-free clustering with Q-learning for wireless sensor networks,” in Proceedings of International Conference on Distributed Computing Systems, 2009, pp. 441–449.
- ↑ G. Kaur, P. Chanak, and M. Bhattacharya, “Energy-Efficient Intelligent Routing Scheme for IoT-Enabled WSNs,” IEEE Internet of Things Journal, vol. 8, no. 14, pp. 11440–11449, Jul 2021.
- ↑ W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “An application-specific protocol architecture for wireless microsensor networks,” IEEE Transactions on Wireless Communications, vol. 1, no. 4, pp. 660–670, Oct 2002.
- ↑ R. V. Kulkarni, A. Forster, and G. K. Venayagamoorthy, “Computational intelligence in wireless sensor networks: A survey,” IEEE Communications Surveys and Tutorials, vol. 13, no. 1, pp. 68–96, 2011.
- ↑ V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. A. Riedmiller, “Playing Atari with Deep Reinforcement Learning,” ArXiv, vol. abs/1312.5602, 2013.








![{\displaystyle L_{i}(w_{i})=\mathrm {E} _{s,a,r,s'\sim D_{i}}\left[{\Bigl (}r+\gamma {\underset {a'}{max}}Q(s',a';w_{i}^{\text{-}})-Q(s,a;w_{i}){\Bigr )}^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c3f606f6db89dcc362aaa229f07c644c3ee6d8e)